Example #1: Bilateral tumor model
Consider an experimental setting utilizing a murine model with bilateral subcutaneous tumor implantation, where each subject bears two distinct tumor sites: one on the left flank and one on the right flank.
Due to intrinsic biological variability and microenvironmental factors, these neoplastic lesions demonstrate heterogeneous growth kinetics, resulting in significant inter-tumor volume variability at the initiation of therapeutic intervention. The following patterns are commonly observed:- Asymmetric growth with predominant left flank tumor burden;
- Asymmetric growth with predominant right flank tumor burden;
- Symmetric growth with comparable bilateral tumor volumes;
Given that treatment efficacy is correlated with initial tumor burden, a critical experimental design consideration emerges:
How can experimental subjects be optimally stratified into treatment cohorts to ensure equivalent mean tumor volumes across both tumor sites, thereby minimizing inter-group variability?
Randomization (random group assignment) is suboptimal for low sample sizes (<12 animal/group). A correct group balancing is a complex challenge with many combinations to be tested.
Below is a comparative analysis of group homogeneity achieved through balancing optimization:
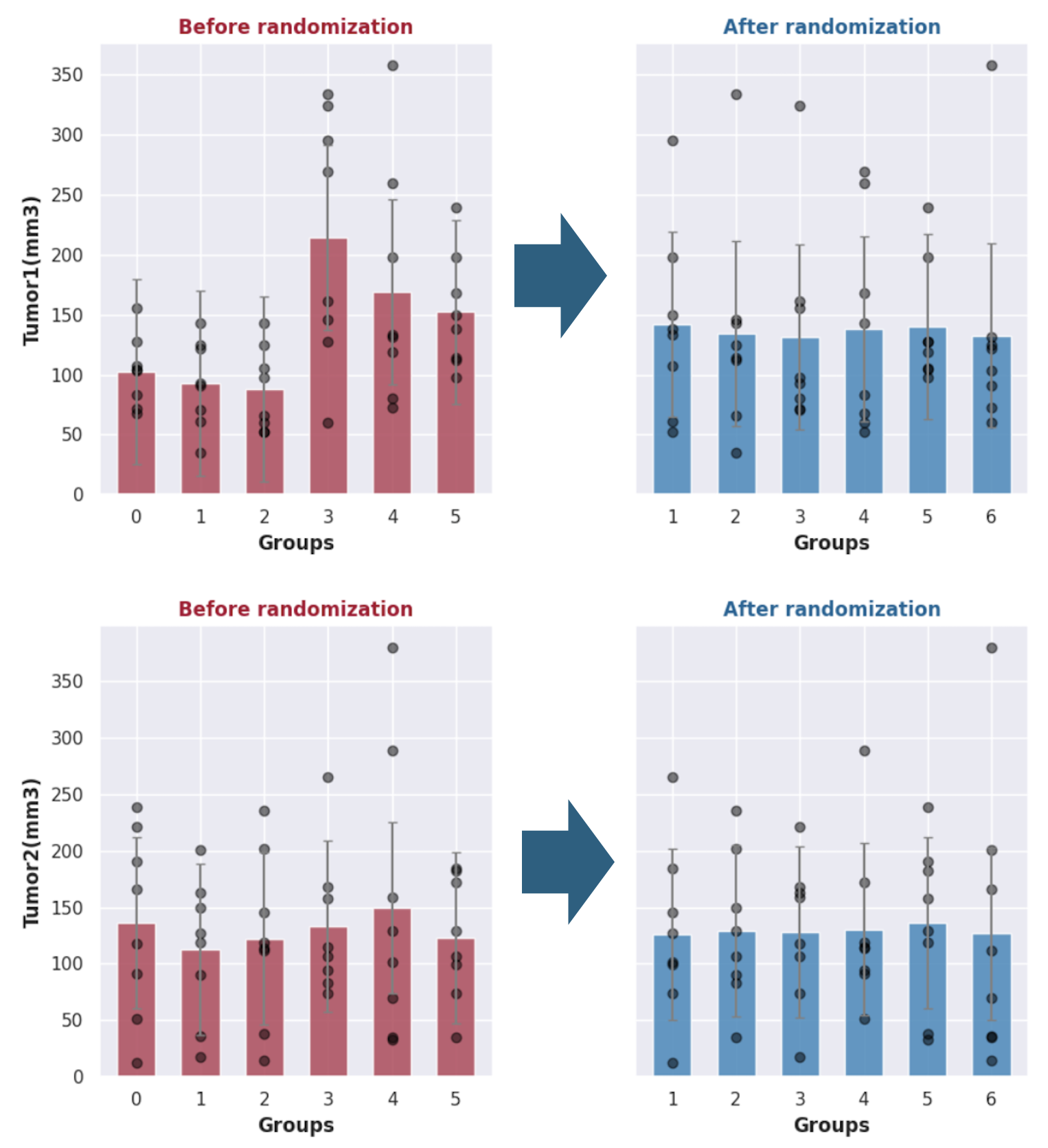
The data demonstrate significantly improved inter-group homogeneity on both tumors compared to manual randomization.
Example #2: Adding another variable, blood pressure
 +
+

Consider an experimental with a bilateral tumor model (like above) but you would like to also homogeneize with the blood pressure because it is also known to impact the efficacy of the treatment.
The problem becomes even more complex, as you now have 3 covariates:
- the size of the left tumor,
- the size of the right tumor,
- the blood pressure.
Randomization (random assignment) is suboptimal for low scale experiment. But this is somehing that randmice can handle easily but randomly testing multiple combinations until it finds the optimum.
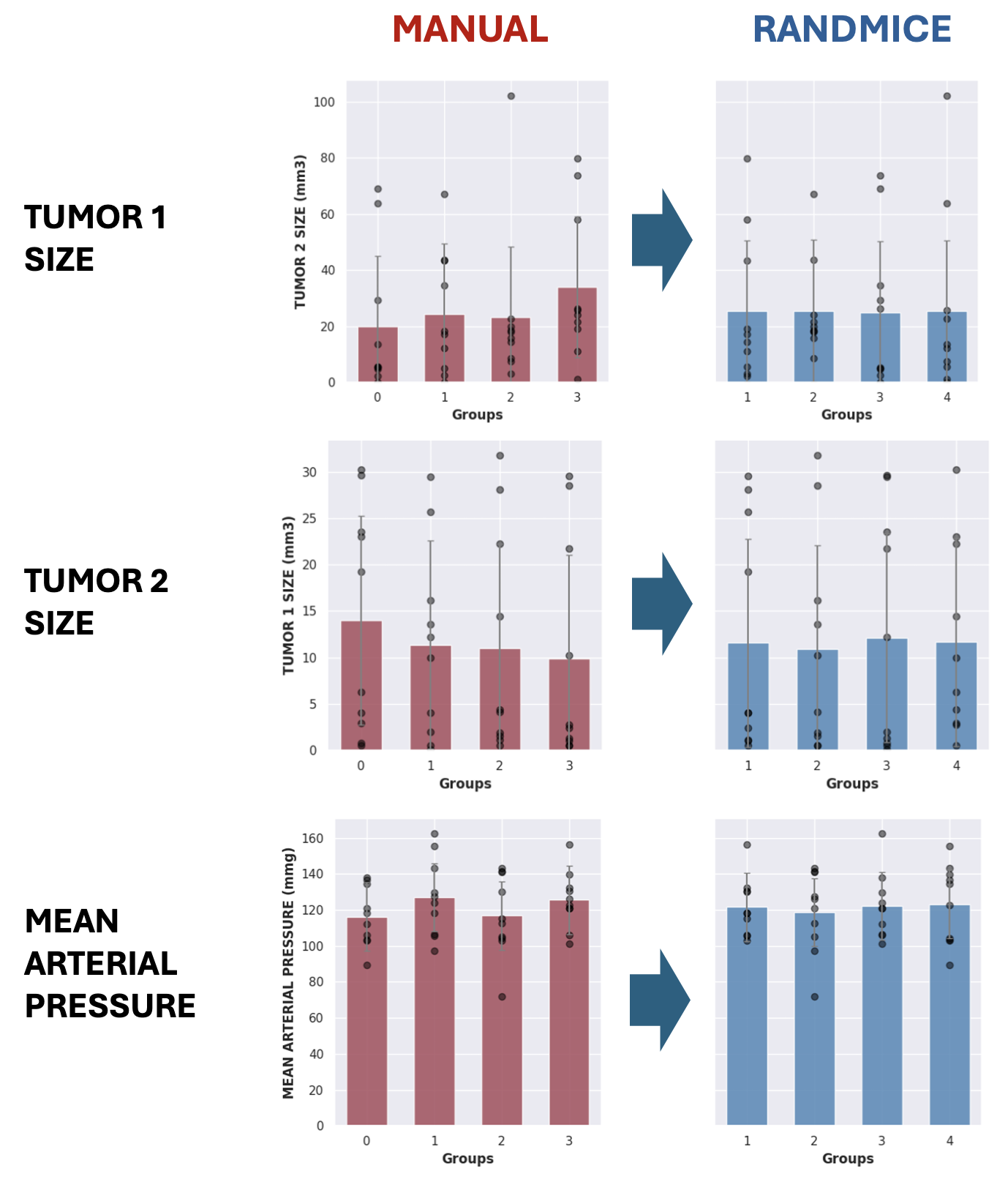
The data demonstrate significantly improved inter-group homogeneity on both tumors and blood pressure compared to pure randomization.